Euler’s method, named after Leonhard Euler, is a popular numerical procedure of mathematics and computation science to find the solution of ordinary differential equation or initial value problems. It is a first order method in which local error is proportional to the square of step size whereas global error is proportional to the step size.
Considered the simplest method to solve ordinary differential equation, Euler’s method finds a clear expression for y with respect to a finite number of elementary functions of x. Here, the initial values of x and y are already known.
The algorithm/flowchart and C program of this method has already been discussed in earlier tutorials. Here’s a program code for Euler’s method in MATLAB along with its mathematical derivation and numerical example.
Derivation of Euler’s Method:
Euler’s method is basically derived from Taylor’s Expansion of a function y around t0. The equation to satisfy this condition is given as:
y(t0 + h) = y(t0) + hy’(t0) + ½ h2 y’’ (t0) + 0 ( h3 )
As per differential equation, y’ = f( t, y). Substituting this in Taylor’s Expansion and neglecting the terms with higher order (or power), we get:
y’(t0) = [y( t0 + h) – y(t0)]/ h
which is the forward finite difference formula of Euler’s method.
Formulation of Euler’s Method:
Consider an initial value problem as below:
y’(t) = f(t, y(t)), y(t0) = y0
In order to find out the approximate solution of this problem, adopt a size of steps ‘h’ such that:
tn = t n-1 + h and tn = t0 + nh.
Now, it can be written that:
yn+1 = yn + hf( tn, yn).
The value of yn is the approximation of solution to the ordinary differential equation (ODE) at time tn. This approach is used to write the program for Euler’s method in Matlab.
Euler’s Method in MATLAB:
%function t=t(n,t0,t1,y0)
function y=y(n,t0,t1,y0)
h=(t1-t0)/n;
t(1)=t0;
y(1)=y0;
for i=1:n
t(i+1)=t(i)+h;
y(i+1)=y(i)+h*ex(t(i),y(i));
end;
V=[t',y']
plot(t,y)
title(' Euler Method')
This code for Euler’s method in Matlab finds out the value of step size (i.e. h) on the basis of initial and final value given in the problem and the total number of iteration. After that, each intermediate values of y are estimated based on Euler’s equation.
Finally, the program finds the required value of y. Here’s a sample screenshot of this program on MATLAB’s Command Window.
The screenshot below is the graphical output of Euler’s MATLAB program.
How to run program of Euler’s method in MATLAB?
- Copy the aforementioned source code to a new MATLAB file and save it as m. For example: euler.m.
- Create another MATLAB file, named ex.m. The file must contain the function to be approximated in standard MATLAB syntax. For example, if y = (t2 – x2) sinx is to be solved, the content of ex.m file will be:
%x is a function of t and y is the first derivative x'(t)
function y=y(t,x)
y=(t^2-x^2)*sin (x);
- Go to MATLAB command window, and write euler(n, t0, t1, y0) and return, where y(t0) = y0 is the initial condition, t0 and t1 are the initial and final points, and n is the number of t-values.
- Finally, the graph of the problem along with the numerical solution (as shown in the two screenshots above) will be displayed.
Euler’s Method Numerical Example:
As a numerical example of Euler’s method, we’re going to analyze numerically the above program of Euler’s method in Matlab. The question here is:
Using Euler’s method, approximate y(4) using the initial value problem given below:
y’ = y, y(0) = 1
Solution:
Choose the size of step as h = 1. The equation used in Euler’s method is:
yn+1 = yn + h f( tn, yn)
where, f( tn, yn) = y
Now,
f( t0, y0 ) = f( 0, 1) = 1
h f(y0) = 1 * 1 = 1
Again,
y 0 + h f(y0) = y1 = 1 + 1 * 1 = 2
Repeating above steps for y2, y3 and y4 :
y 2 = y1 + h f(y1) = 2 +1 * 2 = 4
y 3 = y2 + h f(y2) = 4+1 * 4 = 8
y 4 = y3+ h f(y2) = 8 +1 * 8 = 16
All these calculation can be presented in a tabular format:
Finally, the graphical representation of this problem is given below:
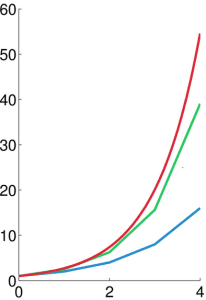
If you have any questions regarding Euler’s method, its MATLAB code, or anything else relevant, bring them up from the comments section below. You can find more Numerical methods tutorial using MATLAB here.