Euler’s Method in C Program is a numerical method that is used to solve nonlinear differential equations. In this article, I will explain how to solve a differential equation by Euler’s method in C. Euler’s method is a simple technique and it is used for finding the roots of a function. When we use this method we don’t require the derivatives of the function. This method is most efficient when the function is known or estimated.
Solving an ordinary differential equation (ODE) or initial value problem means finding a clear expression for y in terms of a finite number of elementary functions of x. Euler’s method is one of the simplest methods for the numerical solution of such an equation or problem. This C program for Euler’s method considers ordinary differential equations, and the initial values of x and y are known.
Mathematically, here, the curve of the solution is approximated by a sequence of short lines i.e. by the tangent line in each interval. (Derivation) Using this information, the value of the value of ‘yn’ corresponding to the value of ‘xn‘ is to determined by dividing the length (xn – x) into n strips.
Therefore, strip width= (xn – x)/n and xn=x0+ nh.
Again, if m be the slope of the curve at point, y1= y0 + m(x0 , yo)h.
Similarly, values of all the intermediate y can be found out.
Below is a source code for Euler’s method in C to solve the ordinary differential equation dy/dx = x+y. It asks for the value of of x0 , y0 ,xn and h. The value of slope at different points is calculated using the function ‘fun’.
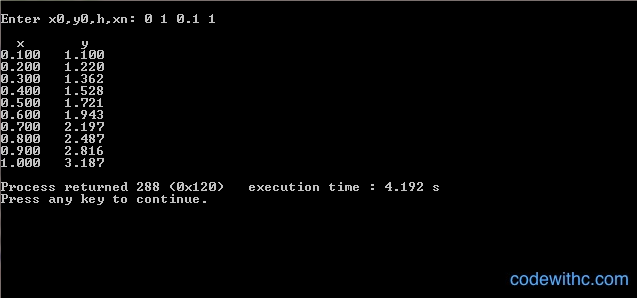
The values of y are calculated in while loop which runs till the initial value of x is not equal to the final value. All the values of ‘y’ at corresponding ‘x’ are shown in the output screen.
dy/dx = x+y
Source Code for Euler’s Method in C:
#include<stdio.h>
float fun(float x,float y)
{
float f;
f=x+y;
return f;
}
main()
{
float a,b,x,y,h,t,k;
printf("\nEnter x0,y0,h,xn: ");
scanf("%f%f%f%f",&a,&b,&h,&t);
x=a;
y=b;
printf("\n x\t y\n");
while(x<=t)
{
k=h*fun(x,y);
y=y+k;
x=x+h;
printf("%0.3f\t%0.3f\n",x,y);
}
}
Input/Output:
Also see,
Euler’s Method Matlab Program
Euler’s Method Algorithm/Flowchart
Numerical Methods Tutorial Compilation
Euler’s method is unarguably very very simple, but it cannot be considered as one of the best approach for to find the solution of initial value problems. It is considered to be very slow, and hence it was later modified in the name of Modified Euler’s Method.
It is a numerical integration method which is used to solve the initial value problem. It is a special case of Runge–Kutta method. The main idea behind this method is to use the current approximation solution and the previous approximation solution to compute the next approximation solution.
The Euler’s method code code in this post needs to be compiled in Code::Blocks. It is well-tested and is bug-free. Any questions related to Euler’s method, or its source code in C presented above, can be mentioned and discussed in the comments.







