Shooting method is a famous method for numerical solution of second order differential equation when boundary condition is known. In this tutorial, we’re going to write a program for Shooting method in C with sample output and working procedure of the method. Shooting method converts the given boundary value problem into initial value problem and solves the problem by using Runge Kutt-4 method.
The working procedure of C program for shooting method is given below:
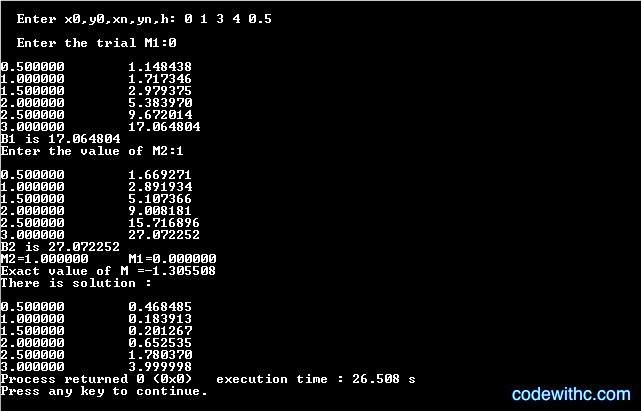
- As the user executes the program, it asks for boundary values i.e. initial value of x (x0), initial value of y (y0), final value of x (xn), final value of y (yn) and the value of increment (h).
- The second step of calculation is to convert this boundary value problem into initial value problem.
- After the conversion into initial value problem, the user has to input the initial guess value of z (M1) which is known as shooting.
- Using this guess value of z, the program calculates intermediate values of z & y are calculated. The final value of y obtained is assigned as B1 in the source code.
- Again, the user has to shoot i.e. the shooting method program asks second initial guess value of z (M2).
- Using M2, new values of y and z are calculated. The final value of y obtained in second guess is assigned as B2 in the program.
- (M1, B1), (M2, B2), and ( y0, z0 ) are assumed to be collinear in this C program and value of z0 determined using following equation,
(B2-B1)/(M2-M1) = (z0-B2)/(y0-M2)
- Using this new and exact value of z, intermediate values are calculated using Runge Kuttta Method.
- Finally, the program prints the result upto 6 decimal places.
Source Code for Shooting Method in C:
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
float f1(float x,float y,float z)
{
return(z);
}
float f2(float x,float y,float z)
{
return(x+y);
}
float shoot(float x0,float y0,float z0,float xn,float h,int p)
{
float x,y,z,k1,k2,k3,k4,l1,l2,l3,l4,k,l,x1,y1,z1;
x=x0;
y=y0;
z=z0;
do
{
k1=h*f1(x,y,z);
l1=h*f2(x,y,z);
k2=h*f1(x+h/2.0,y+k1/2.0,z+l1/2.0);
l2=h*f2(x+h/2.0,y+k1/2.0,z+l1/2.0);
k3=h*f1(x+h/2.0,y+k2/2.0,z+l2/2.0);
l3=h*f2(x+h/2.0,y+k2/2.0,z+l2/2.0);
k4=h*f1(x+h,y+k3,z+l3);
l4=h*f2(x+h,y+k3,z+l3);
l=1/6.0*(l1+2*l2+2*l3+l4);
k=1/6.0*(k1+2*k2+2*k3+k4);
y1=y+k;
x1=x+h;
z1=z+l;
x=x1;
y=y1;
z=z1;
if(p==1)
{
printf("\n%f\t%f",x,y);
}
}while(x<xn);
return(y);
}
main()
{
float x0,y0,h,xn,yn,z0,m1,m2,m3,b,b1,b2,b3,e;
int p=0;
printf("\n Enter x0,y0,xn,yn,h:");
scanf("%f%f%f%f%f",&x0,&y0,&xn,&yn,&h);
printf("\n Enter the trial M1:");
scanf("%f",&m1);
b=yn;
z0=m1;
b1=shoot(x0,y0,z0,xn,h,p=1);
printf("\nB1 is %f",b1);
if(fabs(b1-b)<0.00005)
{
printf("\n The value of x and respective z are:\n");
e=shoot(x0,y0,z0,xn,h,p=1);
return(0);
}
else
{
printf("\nEnter the value of M2:");
scanf("%f",&m2);
z0=m2;
b2=shoot(x0,y0,z0,xn,h,p=1);
printf("\nB2 is %f",b2);
}
if(fabs(b2-b)<0.00005)
{
printf("\n The value of x and respective z are\n");
e= shoot(x0,y0,z0,xn,h,p=1);
return(0);
}
else
{
printf("\nM2=%f\tM1=%f",m2,m1);
m3=m2+(((m2-m1)*(b-b2))/(1.0*(b2-b1)));
if(b1-b2==0)
exit(0);
printf("\nExact value of M =%f",m3);
z0=m3;
b3=shoot(x0,y0,z0,xn,h,p=0);
}
if(fabs(b3-b)<0.000005)
{
printf("\nThere is solution :\n");
e=shoot(x0,y0,z0,xn,h,p=1);
exit(0);
}
do
{
m1=m2;
m2=m3;
b1=b2;
b2=b3;
m3=m2+(((m2-m1)*(b-b2))/(1.0*(b2-b1)));
z0=m3;
b3=shoot(x0,y0,z0,xn,h,p=0);
}while(fabs(b3-b)<0.0005);
z0=m3;
e=shoot(x0,y0,z0,xn,h,p=1);
}
Input/Output:
Also see,
Numerical Methods Tutorial Compilation
The aforementioned C source code for shooting method is a very useful program for solving the second order differential equation when the problem has the nature of boundary value problem. The coding is a bit long, but it is simple to understand with the use of few functions for respective purposes.







