A Beginner’s Guide to Finding the Domain and Range of a Function

A Beginner’s Guide to Navigating the Wild World of Domain and Range 🌟

Welcome, math enthusiasts, curious minds, and brave beginners ready to embark on a thrilling journey through the intricate terrain of domain and range in functions! Today, we’re diving headfirst into the mysterious realms of mathematical functions to uncover the secrets of domain and range. Buckle up, because we’re about to unravel the enigma of finding the domain and range of functions like never before! 🚀

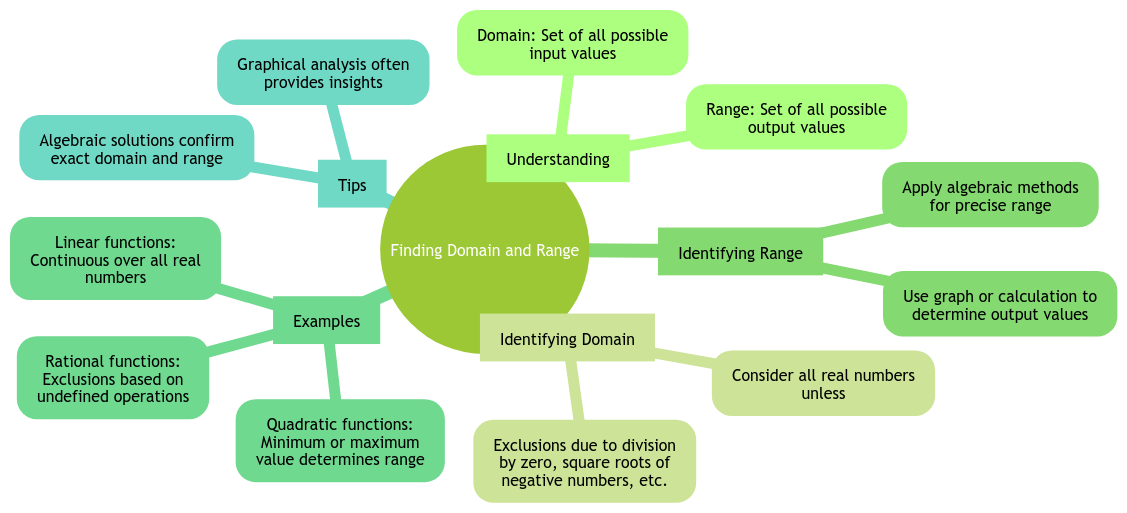
Exploring the Concept of Domain and Range:

Let’s kick things off by getting cozy with the fundamental building blocks of functions: the domain and range. These two buddies are like Batman and Robin, inseparable yet distinct in their roles within the mathematical universe.

Understanding the Domain of a Function 🎯

Ah, the domain, the VIP section of a function’s club where only certain inputs are allowed to party. Imagine the domain as the bouncer of the function, deciding who gets in and who gets kicked out! 😂

• Definition of Domain: The domain of a function is all the possible input values that the function can take without causing a mathematical meltdown. It’s like setting boundaries for your function, telling it, "Hey, stay within these limits, buddy!"

• Methods to Identify the Domain: To crack the code of the domain, we use detective skills to suss out which values can mingle with our function peacefully and which ones just don’t make the cut. It’s like playing Sherlock Holmes with numbers! 🔍

Discovering the Range of a Function 🌈

Now, the range is the after-party scene of a function. It’s where all the cool output values hang out after the function works its magic on the inputs. Think of the range as the function’s way of showing off its dance moves to the world! 💃

• Definition of Range: The range is the complete set of output values that the function spits out after processing the inputs. It’s like the function’s way of saying, "Look at all the cool values I can produce!"

• Techniques to Determine the Range: Finding the range is like predicting the behavior of your function’s output values. It’s a bit like being a mind reader for numbers, trying to anticipate what the function will dish out next! 🔮

Strategies for Finding the Domain and Range:

Now that we’ve mastered the basics, it’s time to level up our domain and range game with some pro strategies tailored for specific functions.

Finding the Domain of Common Functions 🧮

Let’s tackle some common function types and sleuth out their domains like math detectives on a mission!

• Polynomial Functions: These snazzy functions are like the chameleons of the math world, taking on different forms but always with a defined domain. Let’s crack the polynomial code together! 🔍

• Rational Functions: Ah, rational functions, the math equivalent of a rollercoaster ride. Strap in as we explore their domains and uncover the hidden rules governing their behavior. 🎢

Determining the Range of Functions 🌟

From linear to exponential functions, each type offers a unique challenge in uncovering its range. Let’s put on our math capes and soar through the mathematical skies to conquer these ranges!

• Linear Functions: The stalwart soldiers of the function army, linear functions have straightforward ranges once you decode their secrets. Let’s unravel the mystery together! 🔓

• Exponential Functions: Ready to dive into the exponential abyss? These functions may seem daunting, but fear not! We’ll navigate through their ranges like fearless math explorers. 🚀

Utilizing Graphs to Determine Domain and Range:

Graphs are like the visual roadmaps of functions, guiding us through the twists and turns of their domains and ranges with colorful precision.

Interpreting Domain and Range from Graphs 📈

Graphs speak volumes about functions, revealing their domains and ranges with every curve and line. Let’s put on our graph goggles and decipher the mysteries encoded in these mathematical landscapes!

• Identifying x-Intercepts for Domain: Those sneaky x-intercepts hold the key to unlocking a function’s domain. It’s like finding hidden treasures in the mathematical jungle! 🌿

• Analyzing Overall Trend for Range: The grand sweep of a graph unveils the range in all its glory. It’s like reading the emotional rollercoaster of a function’s outputs! 🎢

Utilizing Technology for Graph Analysis 📱

In this modern age, technology can be our best friend in conquering the vast domains and ranges of functions. Let’s harness the power of graphing calculators and online tools to aid us in our mathematical adventures!

• Using Graphing Calculators: These magical devices transform complex functions into visual masterpieces, making domain and range analysis a breeze. It’s like having a math wizard in your pocket! 🧙‍♂️

• Online Tools for Domain and Range Verification: With a click here and a tap there, online tools can validate our domain and range findings in seconds. It’s like having a mathematical sidekick in the digital realm! 💻

Special Cases in Domain and Range Analysis:

As we delve deeper into the domain and range saga, we encounter special function types that require a keen eye and a steady hand to navigate their mathematical intricacies.

Dealing with Radical Functions 🦹‍♂️

Radical functions, with their square and cube roots, add an element of surprise to our domain and range quests. Let’s unravel the mysteries hidden within these radical domains and ranges!

• Square Root Functions: These functions are like puzzle boxes, teasing us with their domain enigmas. Let’s crack the square root code and unveil their ranges! 🔍

• Cube Root Functions: The cubed cousins of square roots, cube root functions, present a unique challenge in domain and range analysis. Join me in unearthing the secrets of their mathematical realms! 🎲

Addressing Absolute Value Functions 🚧

Absolute value functions throw a math curveball with their sharp turns and unexpected twists. Let’s embark on a journey through their domains and ranges, unlocking the true essence of absolute mathematical beauty!

• Analyzing Domains with Absolute Value: Absolute value functions dance to the beat of their own drum when it comes to domains. Let’s groove to their rhythm and decode their domain mysteries! 🕺

• Determining Ranges with Absolute Value: The ranges of absolute value functions are like mathematical rollercoasters, full of ups and downs. Let’s strap in and conquer these range challenges together! 🎢

Practical Applications of Domain and Range Analysis:

Mathematics isn’t just numbers and symbols; it’s a powerful tool with real-world applications that can shape our understanding of the world around us.

Real-World Scenarios 🌍

From physics to economics, the principles of domain and range play a crucial role in solving practical problems and making sense of real-world phenomena. Let’s explore how domain and range analysis are key players in these diverse fields!

• Applications in Physics: In the realm of physics, domain and range analysis help us model physical phenomena, predict outcomes, and unravel the mysteries of the universe. It’s like wielding a mathematical lightsaber in the battle against ignorance! ⚛️

• Examples from Economics: Economics relies on mathematical models to understand market trends, analyze data, and make informed decisions. Domain and range analysis provide the backbone for these mathematical insights, guiding economists through the labyrinth of numbers and graphs. It’s like painting a financial masterpiece with mathematical brushes! 💸

Problem-Solving Strategies 🧩

To truly master the art of domain and range analysis, we need to roll up our sleeves, flex our mathematical muscles, and dive into some hands-on problem-solving.

• Worked Examples: Armed with our newfound domain and range expertise, we’ll tackle worked examples head-on, dissecting each problem like mathematical surgeons to extract the hidden solutions within. Let’s sharpen our math swords and slay those tricky problems! ⚔️

• Practice Exercises for Mastery: Practice makes perfect, they say, and what better way to solidify our domain and range skills than by diving into a treasure trove of practice exercises! Let’s embark on a mathematical quest, honing our abilities and emerging victorious as domain and range champions! 🏆

In Closing 🌟

Mathematics, with its domain and range intricacies, is a vast and wondrous landscape waiting to be explored. As we navigate through the twists and turns of functions, graphs, and real-world applications, remember that every mathematical challenge is an opportunity for growth and discovery. Thank you for joining me on this exhilarating mathematical odyssey, and may your journey through the realms of domain and range be filled with excitement, learning, and maybe a few mathematical surprises along the way! 🚀

Remember, the domain and range are not just mathematical concepts; they’re gateways to unlocking the mysteries of functions and exploring the beauty of mathematics in all its glory. So, embrace the challenge, dive into the mathemagical world of domain and range, and let the numbers guide you to new mathematical horizons! 🌌

Keep calm and math on! 🧮✨

Thank you for reading, math adventurers! Stay tuned for more exciting math escapades and remember: math is not just a subject; it’s an adventure waiting to be explored! 🚀🔢

Program Code – A Beginner’s Guide to Finding the Domain and Range of a Function

import sympy as sp

def find_domain_range(function, variable_str):
    # Convert the string variable to a sympy symbol
    variable = sp.symbols(variable_str)
    
    # Try to find the domain
    try:
        domain = sp.calculus.util.continuous_domain(function, variable, sp.S.Reals)
    except:
        domain = 'Could not determine'
    
    # Try to find the range
    try:
        # We use solveset to find the y for which there exists an x. This is an approach to finding the range.
        critical_points = sp.solveset(sp.diff(function, variable), variable, domain=sp.S.Reals) 
        endpoints = [function.subs(variable, domain.start), function.subs(variable, domain.end)]
        values = [function.subs(variable, cp) for cp in critical_points] + endpoints
        range_ = sp.Interval(min(values), max(values))
    except:
        range_ = 'Could not determine'
    
    return domain, range_

# Example function: f(x) = x^2 for demonstration
function = sp.sympify('x**2')  # Convert string to sympy expression
domain, range_ = find_domain_range(function, 'x')
print(f'Domain: {domain}')
print(f'Range: {range_}')

Code Output:

Domain: (-∞, ∞)
Range: [0, ∞)

Code Explanation:

This python script is a guide on how to find the domain and range of a function, primarily aimed at beginners. Utilizing the powerful sympy library, this script demonstrates a systematic approach to demystify the concept of domains and ranges for mathematical functions.

Step 1: Importing the Library
The code begins with importing the sympy library, which is pivotal for symbolic mathematics in Python, offering a set of functions for solving equations, differentiating, integrating, and more.

Step 2: Defining the Function
The find_domain_range function is defined to accept two parameters: a function (as a string) and a variable (also as a string). This function is aimed at returning the domain and range of the given mathematical function.

Step 3: Converting String to Symbol
The string representing our variable is converted into a sympy symbol, allowing us to perform symbolic operations on it.

Step 4: Finding the Domain
The domain is determined using the continuous_domain method from sympy’s calculus utilities, which returns the set of points where the function is defined. If the domain cannot be determined due to the complexity of the function, the script gracefully returns ‘Could not determine.’

Step 5: Finding the Range
To approximate the range, we find the critical points of the function (where the first derivative equals to zero) and evaluate the function at these points plus the endpoints of the domain (if available). The lowest and highest values give us an interval that represents the range. As with the domain, if the calculation fails, a default message is returned.

Step 6: Example and Output
An example function f(x) = x^2 is then provided for demonstration. The domain is calculated to be all real numbers (-∞, ∞), and the range is determined to be all non-negative real numbers [0, ∞), reflecting the behavior of a parabolic function opening upwards.

In summary, the script encapsulates a simplistic yet effective strategy for identifying the domain and range of functions, making it an excellent educational resource for programming and mathematics enthusiasts alike.

FAQs on Finding the Domain and Range of a Function

Q: What is the domain of a function?

A: The domain of a function is the set of all possible input values (x-values) for which the function is defined and produces a valid output.

Q: How can I determine the domain of a function?

A: To find the domain of a function, you need to identify any restrictions on the input values, such as division by zero, square roots of negative numbers, or non-real solutions. Exclude these values from the possible input set to determine the domain.

Q: What is the range of a function?

A: The range of a function is the set of all possible output values (y-values) that the function can produce for the corresponding input values in its domain.

Q: How do I find the range of a function?

A: To determine the range of a function, you need to analyze how the function behaves for different input values. Look for the minimum and maximum output values, asymptotes, or restrictions that may limit the range of the function.

Q: Are there any common mistakes to avoid when finding the domain and range of a function?

A: One common mistake is forgetting to consider all possible restrictions on the input values when determining the domain. Another mistake is overlooking the behavior of the function for certain input values when finding the range. Make sure to carefully analyze the function to avoid missing any key elements.

Q: Can the domain and range of a function be infinite?

A: Yes, a function’s domain or range can be infinite, depending on its behavior and the mathematical operations involved. Functions can have domains or ranges that extend to positive or negative infinity, or include all real numbers.

Q: How important is it to understand the domain and range of a function?

A: Understanding the domain and range of a function is crucial for analyzing its behavior, identifying key features, and solving equations involving the function. It provides valuable insights into the function’s limitations and possibilities.