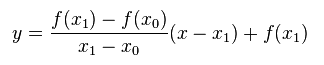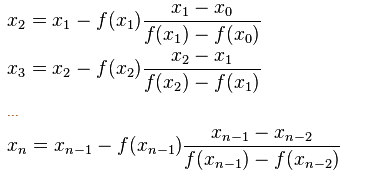Secant method is an iterative tool of mathematics and numerical methods to find the approximate root of polynomial equations. During the course of iteration, this method assumes the function to be approximately linear in the region of interest.
Although secant method was developed independently, it is often considered to be a finite difference approximation of Newton’s method. But, being free from derivative, it is generally used as an alternative to the latter method.
Previously, we talked about secant method vis-à-vis C program and algorithm/flowchart for the method. Here, we’ll go through a program for Secant method in MATLAB along with its mathematical background and a numerical example.
Mathematical Derivation of Secant Method:
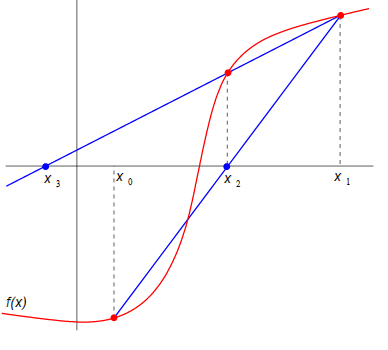
Consider a curve f(x) = 0 as shown in the figure below:
Secant method estimates the point of intersection of the curve and the X- axis (i.e. root of the equation that represents the curve) as exactly as possible. For that, it uses succession of roots of secant line in the curve.
Assume x0 and x1 to be the initial guess values, and construct a secant line to the curve through (x0, f(x0)) and (x1, f(x1)). The equation of this secant line is given by:
If x be the root of the given equation, it must satisfy: f(x) = 0 or y= 0. Substituting y = 0 in the above equation, and solving for x, we get:
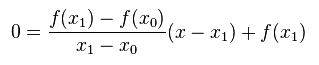
Now, considering this new x as x2, and repeating the same process for x2, x3, x4, . . . . we end up with the following expressions:
This is the required formula which will also be used in the program for secant method in Matlab.
Advantages of Secant Method over other Root Finding Methods:
- Its rate of convergence is more rapid than that of bisection method. So, secant method is considered to be a much faster root finding method.
- In this method, there is no need to find the derivative of the function as in Newton-Raphson method.
Limitations of Secant Method:
- The method fails to converge when f(xn) = f(xn-1)
- If X-axis is tangential to the curve, it may not converge to the solution.
Secant Method in MATLAB:
% Secant Method in MATLAB
a=input('Enter function:','s');
f=inline(a)
x(1)=input('Enter first point of guess interval: ');
x(2)=input('Enter second point of guess interval: ');
n=input('Enter allowed Error in calculation: ');
iteration=0;
for i=3:1000
x(i) = x(i-1) - (f(x(i-1)))*((x(i-1) - x(i-2))/(f(x(i-1)) - f(x(i-2))));
iteration=iteration+1;
if abs((x(i)-x(i-1))/x(i))*100<n
root=x(i)
iteration=iteration
break
end
end
In this program for secant method in Matlab, first the equation to be solved is defined and assigned with a variable ‘a’ using inline( ) library function. Then, the approximate guess values and desired tolerance of error are entered to the program, following the MATLAB syntax.
The program uses the secant formula (aforementioned in the mathematical derivation) to calculate the root of the entered function. Here’s a sample output of the above MATLAB code for secant method:
Secant Method Numerical Example:
Lets perform a numerical analysis of the above program of secant method in MATLAB. The same function f(x) is used here; x0 =0 and x1 = -0.1 are taken as initial approximation, and the allowed error is 0.001.
Here,
f(x) = cos(x) + 2 sin(x) + x2
x0 = 0
x1 = -0.1
For first iteration,
f(x1) = cos(-0.1) + 2 sin(-0.1) + ( -0.1 )2 = 0.8053 and
f(x0) = cos0 + 2 sin0 + 02 = 1
As we know,
x2 = x1 – f(x1)
x2 = 0 + 0.8053 * (-0.1-0)/(0.8053-1)
x2 =0.4136
Similarly, x3 = – 0.5136, and so on…
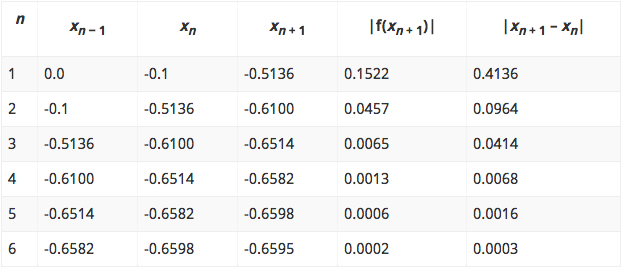
The complete calculation and iteration of secant method (and MATLAB program) for the given function is presented in the table below:
Thus, the root of f(x) = cos(x) + 2 sin(x) + x2 as obtained from secant method as well as its MATLAB program is -0.6595.
Check: f(-0.6585) = cos(-0.6585) + 2 sin(-0.6585) + (-0.6585)2 = 0.0002 (OK).
If you have questions regarding secant method or its MATLAB code, bring them up from the comments section. You can find more Numerical methods tutorial using MATLAB here.