Newton-Raphson method, named after Isaac Newton and Joseph Raphson, is a popular iterative method to find the root of a polynomial equation. It is also known as Newton’s method, and is considered as limiting case of secant method.
Based on the first few terms of Taylor’s series, Newton-Raphson method is more used when the first derivation of the given function/equation is a large value. It is often used to improve the value of the root obtained using other rooting finding methods in Numerical Methods.
We have already discussed C program and algorithm/flowchart for Newton’s method in earlier tutorials. Here, we are going to go through a sample program code for Newton Raphson method in MATLAB, along with a numerical example and theoretical background.
Derivation of Newton-Raphson Method:
The theoretical and mathematical background behind Newton-Raphson method and its MATLAB program (or program in any programming language) is approximation of the given function by tangent line with the help of derivative, after choosing a guess value of root which is reasonably close to the actual root.
The x- intercept of the tangent is calculated by using elementary algebra, and this calculated x-intercept is typically better approximation to the root of the function. This procedure is repeated till the root of desired accuracy is found.
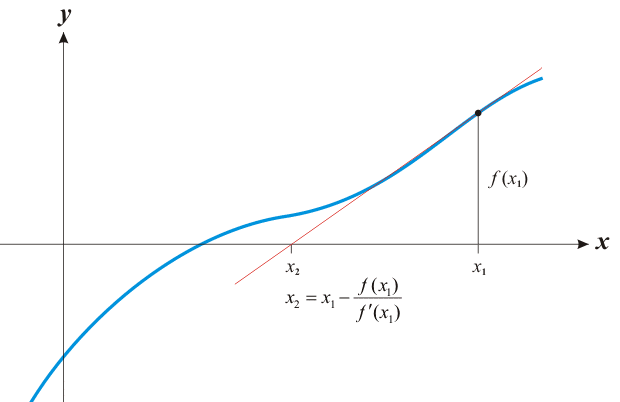
Lets now go through a short mathematical background of Newton’s method. For this, consider a real value function f(x) as shown in the figure below:
Consider x1 to be the initial guess root of the function f(x) which is essentially a differential function. Now, to derive better approximation, a tangent line is drawn as shown in the figure. The equation of this tangent line is given by:
y = f’(x1) (x- x1) + f(x1)
where, f’(x) is the derivative of function f(x).
As shown in the figure, f(x2) = 0 i.e. at x = x2, y=0
Therefore, 0 = f’(x1) (x2– x1) + f(x1)
Solving, x2 = x1 – f(x1) / f’(x1)
Repeating the above process for xn and xn+1 terms of the iteration process, we get the general iteration formula for Newton-Raphson Method as:
xn+1 = xn – f(xn)/f’(xn)
This formula is used in the program code for Newton Raphson method in MATLAB to find new guess roots.
Steps to find root using Newton’s Method:
- Check if the given function is differentiable or not. If the function is not differentiable, Newton’s method cannot be applied.
- Find the first derivative f’(x) of the given function f(x).
- Take an initial guess root of the function, say x1.
- Use Newton’s iteration formula to get new better approximate of the root, say x2
x2 = x1 – f(x1)/f’(x1) - Repeat the process for x3, x4… till the actual root of the function is obtained, fulfilling the tolerance of error.
Newton Raphson Method in MATLAB:
% Program Code of Newton-Raphson Method in MATLAB
a=input('Enter the function in the form of variable x:','s');
x(1)=input('Enter Initial Guess:');
error=input('Enter allowed Error:');
f=inline(a)
dif=diff(sym(a));
d=inline(dif);
for i=1:100
x(i+1)=x(i)-((f(x(i))/d(x(i))));
err(i)=abs((x(i+1)-x(i))/x(i));
if err(i)<error
break
end
end
root=x(i)
In this code for Newton’s method in Matlab, any polynomial function can be given as input. Initially in the program, the input function has been defined and is assigned to a variable ‘a’.
After getting the initial guess value of the root and allowed error, the program, following basic MATLAB syntax, finds out root undergoing iteration procedure as explained in the theory above. Here’s a sample output of this code:
Newton-Raphson Method Example:
Now, lets analyze the above program of Newton-Raphson method in Matlab, taking the same function used in the above program and solving it numerically. The function is to be corrected to 9 decimal places.
Solution:
Given function: x3−x−1 = 0, is differentiable.
The first derivative of f(x) is f’(x) = 3x2 – 1
Lets determine the guess value.
f(1) = 1 -1 -1 = -1 and f(2) = 8 – 2 -1 = 5
Therefore, the root lies in the interval [1, 2]. So, assume x1= 1.5 as the initial guess root of the function f(x) = x3−x−1.
Now,
f(1.5) = 1.53 – 1.5 – 1 = 0.875
f’(1.5) = 3 * 1.52– 1 = 5.750
Using Newton’s iteration formula:
x2 = x1 – f(x1)/f’(x1) = 1.5 – 0.875/5.750 = 1.34782600
The iteration for x3, x4, …. is done similarly.
The table below shows the whole iteration procedure for the given function in the program code for Newton Raphson in MATLAB and this numerical example.
Therefore, x = 1.324717957 is the desired root of the given function, corrected to 9 decimal places. The MATLAB program gives the result x = 1.3252 only, but this value can be improved by improving the value of allowable error entered.
You can find more Numerical methods tutorial using MATLAB here.