Regula Falsi Method, also known as the false position method, is an iterative method of finding the real roots of a function. This method works by substituting test values for unknown quantities, and is the oldest approach to solve equations in mathematics, numerical methods, and engineering. It is a closed bracket-type method with slow rate of convergence.
In earlier tutorials, we’d already gone through a C program and algorithm/flowchart for Regula Falsi method. Here, we’re going to write a program code for Regula Falsi method in Matlab along with its mathematical derivation and a numerical example.
False position method requires two initial guesses, and uses interpolation approach to find roots. Like the bisection method, the process starts with two guess values, say a and b such that f(a) and f(b) are of opposite sign which confirms that the root lies in the interval [a, b].
Derivation of Regula Falsi Method:
Consider a curve having function f(x) = 0 as shown in the figure below:
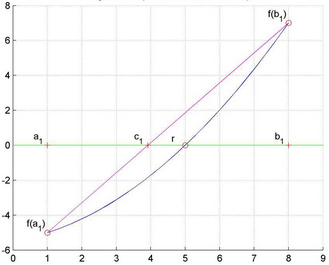
It is required to locate the value of x at a point such that at that point the value of function is equal to zero i.e. x= r and f(r) = 0; ‘r’, which implies to the root of the equation f(x) = 0.
Consider three points on abscissa a1, b1 and c1 with respective ordinates as f(a1), f(b1) and f(c1). From the principle of similar triangle, we have:
[f(b1) – f(a1)] /[ b1 – a1] = [ f(b1) – 0 ] / [ b1 – c1]
Rearranging the terms,
c1 = b1 – f(b1)/[ {f(b1) – f(a1)}/{ b1– a1 }]
if f(c1) = 0, the iteration is stopped, and c1 = r. This is the required formula; the code for Regula Falsi method in MATLAB will be based on these formula and stopping criteria.
In real practice, it is very difficult and takes large number of iteration steps to exactly get f(r) = 0. That is why, we must initially define certain tolerance or allowed error in any program, whether it’s in MATLAB or C.
Conditions for convergence of root:
- When f(a1) and f(b1) have opposite sign, the root lies in the interval [a1, c1]. In this case, the interval is shortened by b1 – c1 and b1 = c1 is set leaving a1 as it is.
- If f(a1) and f(b1) have same sign, the root lies in the interval [ c1, b1]. In this situation, interval is shortened by c1– a1 and a1 = c1 is set leaving b1 as it is.
Regula Falsi Method in MATLAB:
function a = regula_falsi( f )
%for Regula Falsi method
% f is a function for which root to be found.
% asking for the range
f = @(x) x^3 -2*x - 5;
R= input ( 'You are looking for the roots in [ x_min , x_max] :\n');
% check for range
[ nr , mr ] = size( R);
if nr ~= 1 || mr~= 2
disp( 'Input error ..The matrix should be 1x2 matrix')
return
end
% if root lies in the boundary
if feval( f , R( 1,1) )* feval( f , R(1,2)) == 0
if feval( f , R( 1,1) ) == 0
R(1,1)
return
else
feval( f , R(1,2)) == 0
R(1,2)
return
end
end
% condition for convergence
if feval( f , R( 1,1) )* feval( f , R(1,2)) > 0
disp ( 'Either NO root lies in the given range or EVEN no of roots')
disp( 'lie in the given range and hence this method cannot be applied.');
return
end
%error allowed in final answer
tol = abs(input(' Enter the error allowed in the final answer :'));
% no of iterations to be performed
n = input('Enter the maximum number of iterations to be performed :');
%initializing the value of k and matrix X
k=1;
X= zeros(n+1,3);
%initial display of table & initializing values for look
disp(sprintf('\t iterate \t value of x \t error'));
x0= R(1,1); x1= R(1,2); x_disp= x0; err = x1-x0;
disp(sprintf ('\t %3d \t %11.5f \t %11.5f ', 0, x_disp,err));
% iteration loop starts
while k <=n && abs(err) > tol
x = x1 - (x1-x0)/( feval(f,x1)-feval(f,x0) ) *feval(f,x1);%REGULA FALSI formula
if feval(f , x0) * feval(f , x) == 0
x
return
else
if feval(f,x0) * feval(f,x) <0
err = x - x1;
x1 = x;
x_disp=x1;
X(k,2) = x1;
else
err = x-x0;
x0 = x;
x_disp = x0;
X(k,2) = x0;
end
end
% storing values in the form of matrix
X(k,1) = k;
X(k,3) = abs(err);
disp(sprintf ('\t %3d \t %11.5f \t %11.5f ', k, x_disp,err));
k = k + 1;
end
if abs(err) > tol
disp(sprintf ('The final answer obtained after %3d iterations is %10.10f with an error %10.10f \n' , n , X(n,2),X(n,3)))
disp('Try more no of iterations for desired accuracy')
else
disp(sprintf ('The final answer obtained after %3d iterations is %10.10f with an error %10.10f \n' , (k-1) , X((k-1),2),X((k-1),3)))
end
m = menu('would you like to see how the process converges with iteration?',...
'show in graphical form','No thanks..Get me out of this');
switch m
case 1
x=X(1:(k-1),1);
y=X(1:(k-1),3);
plot(x,y)
xlabel (' No of iterations ')
ylabel (' Error ')
title ('Convergence of Regula-Falsi method')
otherwise
return
end
This program for Regula Falsi method in MATLAB finds the root of the function f(x) = x3 – 2x – 5 within the desired limit of accuracy as input by the user. The value of function can be modified and any function can be given as input.
When the program is executed, it asks for the values of initial guess interval, the allowed error and the maximum number of iterations to be performed. The program shows calculated results in each iteration in tabular form. Here’s a sample output of the program is given below:
Regula Falsi Method Numerical Example:
Now, let’s analyze numerically the above program for Regula Falsi method in MATLAB. We have to determine the roots between (2,3) of equation x3 – 2x – 5 = 0, by using Regula Falsi method.
Solution:
Given equation: x3 – 2x – 5 = 0
Therefore, f(x) = x3 – 2x – 5.
Now, f(2) = 23 – 2*2 – 5 = -1 and f(3) = 33 – 2*3 – 5 = 16.
As f(2) and f (3) have opposite sign, it confirms that the root lies in the interval [2, 3].
Now, using the formula discussed in the derivation:
c1 = b1 – f(b1)/[ {f(b1) – f(a1)}/{ b1– a1 }], where, a1 = 2 and b1 = 3
we get, c1 = 2.058
f(c1) = f( 2.058) = -0.4.
So, the root lies in the interval [ 2.058, 3].
Again, using the formula:
c1 = b1 – f(b1)/[ {f(b1) – f(a1)}/{ b1– a1 }], where, a1 = 2.058 and b1 = 3
we get, c1 = 2.081
f(c1 ) = f(2.081) = -0.15.
The process is repeated in similar manner until f(c1 ) comes under the desired degree of accuracy. The following tables shows the iteration procedure in this numerical example and the program of Regula Falsi method in MATLAB.
Thus, the approximate root of the given equation is 2.09, which is somewhat same as that obtained from the MATLAB program.
If you have any questions related to Regula Falsi method, its MATLAB code or mathematical derivation, bring them up from the comments section. You can find more Numerical Methods tutorial using MATLAB here.









