Dijkstra’s Shortest Path Algorithm is a popular algorithm for finding the shortest path between different nodes in a graph. It was proposed in 1956 by a computer scientist named Edsger Wybe Dijkstra. Often used in routing, this algorithm is implemented as a subroutine in another graph algorithm. In this post, I have included a pseudo code and source code for Dijkstra’s Algorithm in C along with a brief introduction to this algorithm.
Dijkstra’s algorithm finds the solution for the single-source shortest path problems only when all the edge weights are non-negative on a weighted, directed graph. In other words, the graph is weighted and directed with the first two integers being the number of vertices and edges that must be followed by pairs of vertices having an edge between them.
In the source code for Dijkstra’s algorithm in C, the inputs are asked as the source, target, and the weight of the path between two nodes. Before going through the source code for Dijkstra’s algorithm in C, here’s a look at the algorithm itself and a pseudo code based on the algorithm.
You can read more about Dijkstra’s algorithm by going to these links: Link 1. Link 2, and here are a couple of Youtube links you can watch if you don’t know much about this algorithm: Link 1. Link 2.
Dijkstra’s Algorithm to Find the Shortest Path:
Let’s fix a node as the initial node; this will be the node at which we are starting. Let the distance of node “Y” be the distance from the initial node to “Y”. Now, in Dijkstra’s algorithm, some initial distance values are assigned, and these values are improved step by step. The algorithm procedure is given below:
- A tentative distance value is assigned to every node; this value is set to zero for the initial node, and to infinity for all other nodes.
- All nodes unvisited are marked, and the initial node is set as current. An unvisited set ( a set of all the unvisited nodes) consisting of all the nodes is created.
- For the current/initial node, take into account all the unvisited nearby nodes, and calculate their tentative distances. Make a comparison of the current assigned value and the newly calculated tentative distance; assign the smaller value. For example: if the current/initial node X was marked with a distance of 4, and the edge connecting it with a nearby neighbor node Y has length 1, then the distance through X to Y will be 4 + 1 = 5. If Y was previously assigned a value greater than 5, then change it to 5. Otherwise, keep the value as it is.
- A visited node is never to be checked again. So, after finishing above steps with all the neighbors of the current node, make that node as visited and remove is from the unvisited set.
- Stop the algorithm if, when planning a route between two specific nodes, the destination node has been marked visited.
- Also, stop the algorithm if, when planning a complete traversal, the smallest tentative distance among the nodes in the unvisited set is infinity. This case is a result of no connection between the initial node and the remaining unvisited nodes.
- Find the unvisited node assigned with the smallest tentative distance value, and this will be the new “current mode”. Go back to step 3, and continue.
Below is an example which further illustrates the Dijkstra’s algorithm aforementioned. Consider a weighted graph as shown:
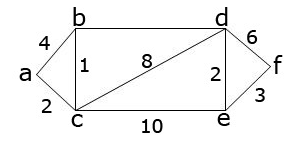
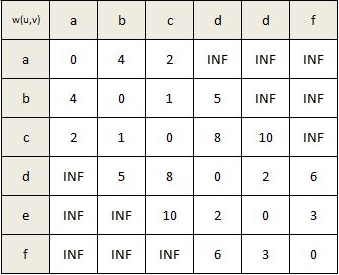
Here, a, b, c, d, e and f are nodes of the graph, and the number between them are the distances of the graph. Now, using Dijkstra’s algorithm we can find the shortest path between initial node a and the remaining vertices. For this, the adjacency matrix of the graph above is:
Pseudo Code for Dijkstra’s Algorithm:
function Dijkstra(Graph, source):
dist[source] := 0 // Distance from source to source
for each vertex v in Graph: // Initializations
if v ≠ source
dist[v] := infinity // Unknown distance function from source to v
previous[v] := undefined // Previous node in optimal path from source
end if
add v to Q // All nodes initially in Q
end for
while Q is not empty: // The main loop
u := vertex in Q with min dist[u] // Source node in first case
remove u from Q
for each neighbor v of u: // where v has not yet been removed from Q.
alt := dist[u] + length(u, v)
if alt < dist[v]: // A shorter path to v has been found
dist[v] := alt
previous[v] := u
end if
end for
end while
return dist[], previous[]
end function
Given above is a sample source code for Dijkstra’s algorithm, referred from Wikipedia. This exact pseudo may have not been used in writing the source code for Dijkstra’s algorithm in C, but it can be used as a reference for coding in any higher level programming language.
Source Code for Dijkstra’s Algorithm in C:
/* Dijkstra's Algorithm in C */
#include<stdio.h>
#include<conio.h>
#include<process.h>
#include<string.h>
#include<math.h>
#define IN 99
#define N 6
int dijkstra(int cost[][N], int source, int target);
int main()
{
int cost[N][N],i,j,w,ch,co;
int source, target,x,y;
printf("\t The Shortest Path Algorithm ( DIJKSTRA'S ALGORITHM in C \n\n");
for(i=1;i< N;i++)
for(j=1;j< N;j++)
cost[i][j] = IN;
for(x=1;x< N;x++)
{
for(y=x+1;y< N;y++)
{
printf("Enter the weight of the path between nodes %d and %d: ",x,y);
scanf("%d",&w);
cost [x][y] = cost[y][x] = w;
}
printf("\n");
}
printf("\nEnter the source:");
scanf("%d", &source);
printf("\nEnter the target");
scanf("%d", &target);
co = dijsktra(cost,source,target);
printf("\nThe Shortest Path: %d",co);
}
int dijsktra(int cost[][N],int source,int target)
{
int dist[N],prev[N],selected[N]={0},i,m,min,start,d,j;
char path[N];
for(i=1;i< N;i++)
{
dist[i] = IN;
prev[i] = -1;
}
start = source;
selected[start]=1;
dist[start] = 0;
while(selected[target] ==0)
{
min = IN;
m = 0;
for(i=1;i< N;i++)
{
d = dist[start] +cost[start][i];
if(d< dist[i]&&selected[i]==0)
{
dist[i] = d;
prev[i] = start;
}
if(min>dist[i] && selected[i]==0)
{
min = dist[i];
m = i;
}
}
start = m;
selected[start] = 1;
}
start = target;
j = 0;
while(start != -1)
{
path[j++] = start+65;
start = prev[start];
}
path[j]='\0';
strrev(path);
printf("%s", path);
return dist[target];
}
Copy and compile the source code above in Code::Blocks IDE. Compiling it on other platforms such as Turbo C may produce errors, and might require some modifications to the code. Go to this link to learn how routing algorithms work.
Also see,
Gaussian Filter Generation
Breadth First Search
Depth First Search
I hope the source code for Dijkstra’s algorithm in C is clear and easy to understand. If you have any queries or doubts regarding Dijkstra’s algorithm, it’s pseudo code or source code, mention them in the comments section below. You can find more C Tutorials here.







Nice explanation. Don’t you think you should start your loop with 0 instead of 1? Since you have 6 nodes for the given example, you could run your loop 6 times. Once again thanks for the code. We truly appreciate it.
Youre the only person who i found that explains and shows up the code for a source->target dijkstra’s algorithm.
thanks man
thank you 🙂
I am looking for a c program to calculate mode for discrete distribution.Can you help ?
plz put a anapshot of output & also it’s graph..
so we understand easily & better..
Hi,
In the graph picture,you’ve missed writing distance between b-d. Plz correct that. And can u plz add some snapshot of program output? I tried entering your graph to your program during run,but it’s giving 0 as output. A snapshot of program is helpful. And I think in each program,at the start of program,if you add a printf statement stating how to use the program,will be helpful. Anyway,I found your site very very helpful. Keep it up!
could you please help me with code for finding shortest path between source and destination pair, using priority vertices, through which graph is to be traversed to reach the destination.
your help means alot to me , i have tried a lot fr dis, could find any correct result , please help me with this @pramesh pudasaini
PLZ EXPLAIN THIS WHOLE CODE…
How do I explain you the WHOLE source code? If you know nothing about Dijkstra’s Algorithm, please go through the post description first. The source code will be relatively easy to understand after that.