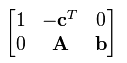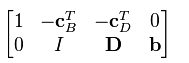Derived by the concept of simplex and suggested by T. S. Motzkin, simplex method is a popular algorithm of mathematical optimization in the field of linear programming. Albeit the method doesn’t work on the principle of simplices (i.e generalization of the notion of a triangle or tetrahedron to arbitrary dimensions), it is interpreted that it operates on simplicial cone and these assume the form of proper simplices with additional constrains.
In this tutorial, we’re going to write a program for Simplex method in MATLAB, discussing its theoretical background and working procedure.
Theoretical Background of Simplex Method:
Consider a standard form of linear program on which the simplex method operates i.e. linear program of form:
Maximize:
cT.x
Subjected to Ax = b , xi ≥ 0
Where, x = (1, x2, x3, x4 0.. . . .. xn) which are the variables in the problem and c = ( 1, c2, c3, c4, . . . . cn ) which are the coefficients of the objective function.
A is a p x n matrix and b = ( b1, b2, b3, . . . . , bp ), bj ≥ 0 which represent the constants.
The linear form can easily be transformed into standard form without loss of generality due to availability of straight forward process of conversion.
The feasible region of above problem in geometric term is:
Ax ≤ b, xi ≥ 0 which is a convex polytope and probably unbound.
Simple Tableaux:
All the linear program in the standard form can be replicated in tableau form. The tableau form of above linear program in standard form is:
In this form, the first row always defines the objective function of the problem and the other remaining rows are defined to represent the constrains of the problem.
This form can be converted into canonical form by arranging the columns of A in such a way that it contains an identity matrix of order p.
When the respective tableau is multiplied by the inverse of the same matrix, the result will tableau in canonical form:
Suppose, the following matrix be tableau in canonical form:
In order to remove the coefficient CTB from objective function, we can apply additional row addition transformation. The result of this pricing out process is:
where, ZB represent the value of objective function at the corresponding feasible solution.
Simplex Method MATLAB Code:
function [ val mat ] = simplex_min(A,C )
% for optimizing given condition 'C' with constraints 'A'
% A is an augmented matrix
% All the constraints are should be of the form L.H.S. <= R.H.S.
% where LHS includes the variable.And the pre-assumed constraint is that all
% the variables are +ve
A =[1 2 3 4 0 0 0; 0 3 2 1 1 0 10; 0 2 5 3 0 1 15]
C = [0 0 0]
[ na ma] = size(A);
[ nc mc] = size(C);
% check for matrix C
if nc ~= 1
disp('Pls check the given objective function.It should be row matrix ')
return
end
% check for the no. of variables in constraints and in objective function
if ma-1 ~= mc
disp('Check the given objective function or augmented matrix')
return
end
%making the initial tebula
X = [ A(:,1:ma-1) eye(na) A(:,ma) ];
X(na+1,:) = zeros(1,na+ma);
X(na+1,1:mc) = -C;% Indicator row.
% initial tebula is ready
%CONDITION : All the elements in the indicator row should be -ve in the final tebula
while sum(X(na+1,1:na+ma-1) > zeros(1,na+ma-1)) ~= 0
% finding the largest matrix element in the co-efficient matrix
xw = X(1:na , 1:na + ma - 1);
[ v1 i1 ] = max(xw);
[ v2 j ] = max(v1);% determining j and hence the pivot coloumn
i = i1(1,j);
Y = X(1:na,na+ma)./X(1:na,j);% determining lowest positive ratio for finding pivot row
a1 = sign(Y);
a1 = a1 + ones(na,1);
y1 = Y.*a1/2;
[ v3 i ] = min(y1);% finding lowest non -ve no
if v3 == 0
ys = sort(y1);
k = 1;
while ys(k,1) <= 0
k = k + 1;
end
b = ys(k,1);
[ i j1 ] = find( y1 == b );
end
X = elimination(X,i,j); % Pls see the function ' elimination '
% finding -ve no in the column matrix
ele = find(sign(X(na+1,1:na+ma-1))== -1);
[ ne me ] = size(ele);
if me == 0
break
else
j = ele(1,1);% fixing pivot column
Y = X(1:na,na+ma)./X(1:na,j);
a1 = sign(Y);
a1 = a1 + ones(na,1);
y1 = Y.*a1/2;
[ v3 i ] = min(y1);
if v3 == 0
ys = sort(y1);
k = 1;
while ys(k,1) <= 0
k = k + 1;
end
b = ys(k,1);
[ i j1 ] = find( y1 == b );
X = elimination(X,i,j);
end
end
% for checking boundedness of solution
for k = 1:na+ma-1
un = sign(X(:,k));
if un == - ones(na+1,1)
disp(' The solution is not bounded')
return
end
end
end
% Obtaining the solution from Final tebula
opt = X( na+1, ma+na);
sol = X(1:na , 1:ma-1);
for k = 1: ma-1
% looking for the column which forms the rrel for matix A
t = roots( [sol(:,k);0] );
[ nt mt ] = size(t);
if t == zeros(nt,1)
mat(1,k) = X(na - nt +1, na+ma);
else
mat(1,k) = 0;
end
end
disp('Co-efficient matrix correspond to optimum solution ')
mat
disp('and optimum value is')
opt
function X = elimination(X,i,j)
% Pivoting (i,j) element of matrix X and eliminating other column
% elements to zero
[ nX mX ] = size( X);
a = X(i,j);
X(i,:) = X(i,:)/a;
for k = 1:nX
if k == i
continue
end
X(k,:) = X(k,:) - X(i,:)*X(k,j);
end
The above Matlab code for Simplex Method doesn’t need any input while running the program. The necessary data of the linear programming are already embedded in the source code. This code solves the following typical problem of linear programming:
Minimization of: Z = -2x – 3y – z
Subjected to:
3x + 2y + z ≤ 10
2x + 2y + z ≤ 15
X, y, z ≥ 0
The sample output of the Matlab program is given below:
If you have any question regarding Simplex method, its Matlab program, or its theory, ask us from the comments section. You can find more Numerical Methods Tutorial using Matlab here.